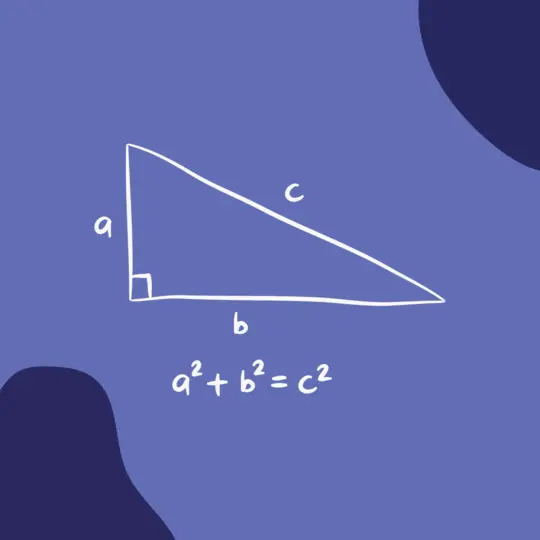Ми раді, що ви присвятили час зануренню у захоплюючу область геометричної математики та розгадці таємниць теореми Піфагора. Без подальшого зволікання давайте заглибимося у вивчення та розуміння цього незвичайного твердження. Квадрат суми катетів дорівнює квадрату довжини гіпотенузи. Крім того, це можна порівняти з польським прислів’ям: «Мудрість — у простоті, як квадрат у математиці». Теорема Піфагора є наріжним каменем геометричної математики і демонструє безліч універсальних додатків. В рамках цього дослідження ми досліджуємо суть цієї теореми, розглянемо його фундаментальні принципи, особливості, застосування як у математичному контексті, так і у повсякденних сценаріях, а також його значення у сфері будівництва та архітектури.
Причини вивчити теорему Піфагора:
- Це виходить за межі простого математичного дискурсу; він служить ключовими воротами до складніших предметів.
- Відкрийте для себе його різноманітну корисність у таких галузях, як фізика, навігація, інформатика та навіть штучний інтелект – інструмент, що виходить за рамки математики.
- Від вимірювання відстаней на картах до формування внутрішнього простору він впливає на наш повсякденний вибір і дії. Відкрийте відчутні переваги, які можна отримати з цієї математичної перлини.
- Без теореми Піфагора багато монументальних споруд просто не існувало б.
Розкриття основної концепції теореми Піфагора: фундаментальні ідеї в одному знімку
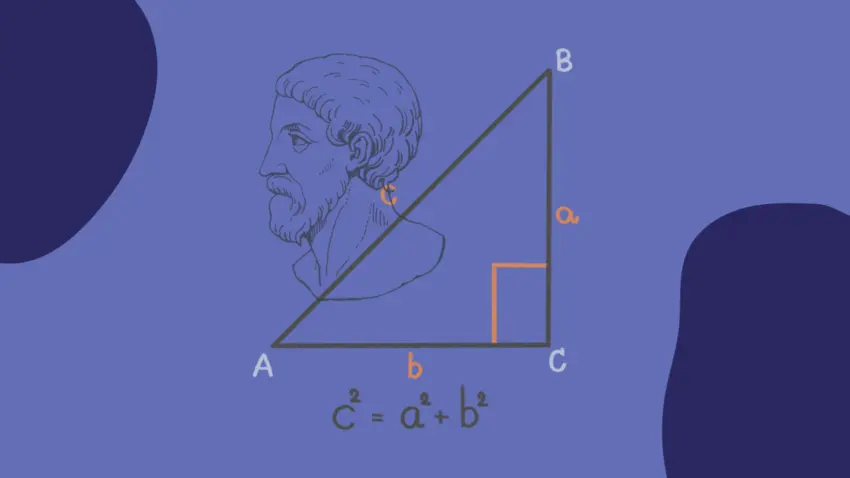
У основі математики, особливо у контексті прямокутних трикутників, лежить теорема Піфагора — основний принцип. Коротко він стверджує, що в таких трикутниках квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів. Математично це виражається рівнянням Піфагора.
с2 = а2 + b2
Це, здавалося б, простий, але дуже потужний вираз служить воротами до розуміння взаємозв'язків між сторонами трикутників, полегшуючи широкий спектр додатків у різних математичних галузях та повсякденних сценаріях. Він діє як метафоричний ключ, що відкриває багатства, приховані в математичній сфері, і спрямовує нас до глибшого розуміння тонкощів геометричного простору.
Інтригуючі факти про теорему Піфагора
Приступаючи до цікавого вивчення загадкових сфер теореми Піфагора, слід зазначити, що її витоки виходять межі Стародавню Грецію. Це математичне диво знайшло визнання та застосування у різних культурах, включаючи єгипетське, китайське та вавілонське товариства.
У Стародавньому Єгипті математики займалися аналогічними геометричними відносинами, підкреслюючи, що концепції, пов'язані з теоремою Піфагора, виходять за межі конкретних регіонів та епох. Китайці також зробили помітний внесок у цю справу, підтвердивши універсальну природу математики та її функцію як міжконтинентальної мови спілкування.
Те, що ми зараз називаємо теоремою Піфагора, мало значення у вавілонській математиці, особливо у дослідженні прямокутних трикутників для практичних додатків у таких галузях, як астрономія та будівництво.
Всі ці приклади підкреслюють, що привабливість теореми Піфагора всеосяжна, перевершуючи тимчасові та просторові обмеження. Вона виникає не просто як фрагмент математичної історії, а і як захоплююча одіссея через багате розмаїття культур та їхню ключову роль у розвитку наукових знань.
Застосування теореми Піфагора в математиці та повсякденних ситуаціях
Основна сфера застосування цієї теореми — розв'язання проблем, пов'язаних з прямокутними трикутниками. Його корисність полягає у полегшенні прямого обчислення довжин сторін трикутника, коли відомі дві інші довжини. Цей ресурс є фундаментальною відправною точкою вивчення взаємодії між кутами й сторонами всередині цього конкретного типу трикутника.
Однак значення теореми Піфагора виходить за межі плоскої геометрії. В галузі математики він також використовується для обчислення відстаней між точками у тривимірному просторі. Це особливо корисно в системі декартових координат, де відстані між точками визначаються за допомогою прямокутних трикутників.
Розв'язання геометричних задач за допомогою теореми Піфагора
У сценаріях вирішення завдань учням доручено ретельно вивчити цю ситуацію, визначити відомі та невідомі значення та згодом використати теорему для отримання рішення.
Акцент виходить за рамки простого запам'ятовування рівнянь та обчислень Піфагора; воно включає розвиток навичок логічного мислення. Учні набувають здатності систематично і точно вирішувати геометричні завдання, навички, що виходять за рамки математики та дозволяють вирішувати завдання у повсякденному житті.
Теорема передбачає подвійну роль: вона служить як математичним інструментом, а й каталізатором розвитку когнітивних навичок, застосовних у різних сферах життя. Він тонко викладає уроки щодо застосування логічного підходу до розв'язання проблем, формуючи гостроту розуму учнів для майбутніх починань.
Історична подорож та еволюція теореми Піфагора
Розуміння, отримане під час історичної подорожі та еволюції теореми Піфагора, вселяє глибоке захоплення цим математичним шедевром. Охоплюючи період від Стародавню Грецію донині, ця теорема як зберігається, а й розвивається, відповідаючи новим викликам і контекстуальним вимогам.
Сьогоднішнє роздум над теоремою Піфагора призводить до усвідомлення того, що вона виходить за рамки єдиного математичного твердження; це фрагмент історії, що не піддається тимчасовим та просторовим обмеженням. Воно є математичною спадщиною, що постійно впливає на наше повсякденне життя, що впливає на архітектуру, інженерію і формує наше сприйняття простору та відносин між об'єктами.
На платформі TeMa на вас чекають онлайн викладачі з математики, готові допомогти вам розгадати секрети цієї захоплюючої наукової галузі. Математичні знання є воротами до безлічі можливостей, а з TeMa навчання стає ще доступнішим. Приготуйтеся до захоплюючої подорожі світом математики, де геометричні загадки є ключем до розуміння навколишнього світу. Успіхів!