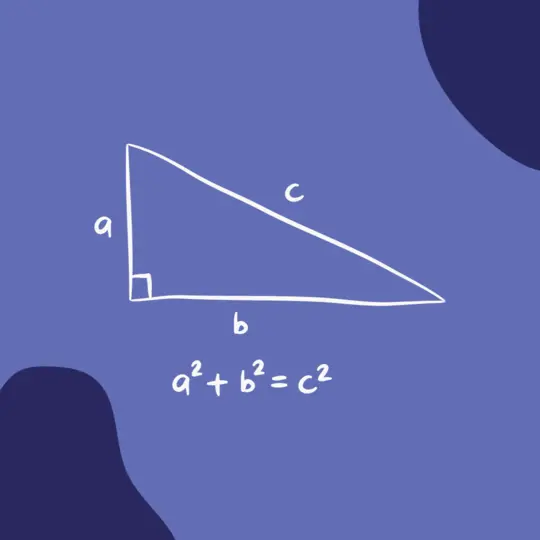We are pleased that you have dedicated time to delve into the captivating realm of geometric mathematics and unravel the mysteries of the Pythagorean Proposition. Without further delay, let's delve more profoundly into the scrutiny and comprehension of this extraordinary assertion. The Pythagorean Proposition stands as the cornerstone of geometric mathematics, exhibiting an array of remarkably versatile applications. Within this scrutiny, we will probe into the core of this proposition, examine its fundamental principles, peculiarities, applications in both mathematical contexts and day-to-day scenarios, and its significance in the realms of construction and architecture.
Reasons to Investigate the Pythagorean Proposition:
- This transcends mere mathematical discourse; it serves as the pivotal gateway to more intricate subjects.
- Uncover its diverse utility in realms such as physics, navigation, computer science, and even artificial intelligence—an instrument that extends beyond the confines of mathematics.
- From gauging distances on maps to shaping interior spaces, it exerts influence on our daily choices and undertakings. Discover the tangible advantages that can be derived from this mathematical gem.
- Devoid of the Pythagorean Proposition, numerous monumental structures would be non-existent.
Unveiling the Core Concept of the Pythagorean Theorem: Fundamental Insights in a Snapshot
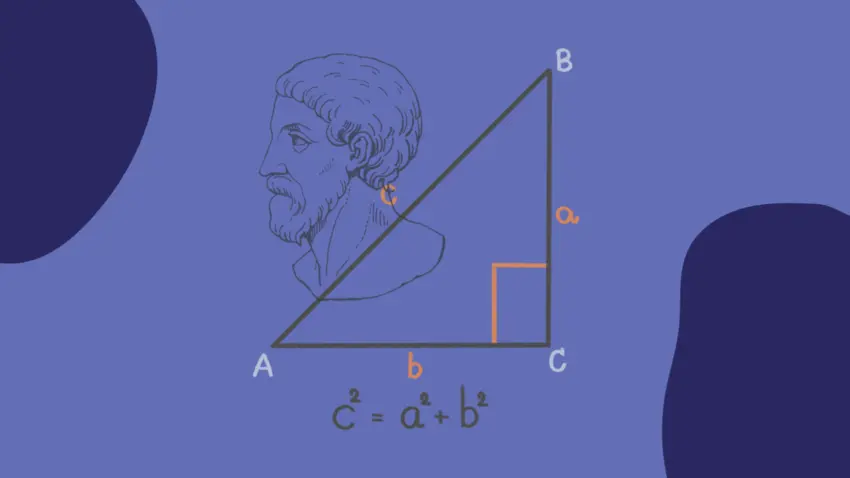
At the heart of mathematics, particularly in the context of right-angled triangles, lies the Pythagorean Theorem—a foundational principle. Succinctly put, it declares that in such triangles, the square of the hypotenuse's length equals the sum of the squares of the lengths of the legs. Mathematically, this is articulated through the Pythagorean equation.
c2 =a2 + b2
This seemingly straightforward yet profoundly potent expression serves as a gateway to comprehending the interrelationships among the sides of triangles, facilitating a broad spectrum of applications across diverse mathematical realms and everyday scenarios. It acts as a metaphorical key, unlocking the riches concealed within the mathematical realm and guiding us towards a deeper grasp of the intricacies of geometric space.
Intriguing Tidbits Regarding the Pythagorean Theorem
Embarking on a captivating exploration into the enigmatic realms of the Pythagorean Theorem, it's noteworthy that its origins extend beyond Ancient Greece. This mathematical marvel found recognition and application in diverse cultures, including Egyptian, Chinese, and Babylonian societies.
In Ancient Egypt, mathematicians engaged with analogous geometric relationships, underscoring that concepts tied to the Pythagorean Theorem transcended specific regions and epochs. The Chinese, too, made distinct contributions to this matter, attesting to the universal nature of mathematics and its function as a cross-continental language of communication.
What we currently identify as the Pythagorean Theorem held significance in Babylonian mathematics, particularly in their exploration of right triangles for practical applications in domains such as astronomy and construction.
All these instances underscore that the allure of the Pythagorean Theorem is all-encompassing, surpassing temporal and spatial confines. It emerges not merely as a fragment of mathematical history, but also as a captivating odyssey through the rich tapestry of cultures and their pivotal roles in advancing scientific knowledge.
Application of the Pythagorean Theorem in Mathematics and Daily Situations
The primary domain where this theorem finds application is in addressing challenges associated with right triangles. Its utility lies in facilitating the straightforward computation of triangle side lengths when two other lengths are known. This resource serves as a fundamental starting point for scrutinizing the interplay between angles and sides within this particular triangle type.
Yet, the significance of the Pythagorean Theorem extends beyond the realm of plane geometry. In the realm of mathematics, it is also deployed to compute distances between points in three-dimensional space. This proves especially beneficial in the Cartesian coordinate system, where distances between points are ascertained through the utilization of right triangles.
Addressing Geometric Challenges through the Pythagorean Theorem
In problem-solving scenarios, students are tasked with a meticulous examination of a given situation, delineating known and unknown values, and subsequently employing the theorem to derive a solution.
The emphasis transcends mere equation memorization and Pythagorean calculations; it encompasses the cultivation of logical thinking skills. Students acquire the ability to approach geometric challenges systematically and precisely, skills that extend beyond mathematics to problem-solving in daily life.
The theorem assumes a dual role, serving not only as a mathematical instrument but also as a catalyst for nurturing cognitive skills applicable across diverse life domains. It subtly imparts lessons in adopting a logical approach to problem resolution, shaping the mental acuity of students for future endeavors.
Historical Journey and Evolution of the Pythagorean Theorem
The insights gleaned from the historical journey and evolution of the Pythagorean theorem instill profound admiration for this mathematical masterpiece. Spanning from Ancient Greece to the contemporary era, the theorem not only endures but evolves to meet new challenges and contextual demands.
Contemplating the Pythagorean Theorem today prompts recognition that it transcends being a singular mathematical proposition; it is a fragment of history that defies temporal and spatial constraints. It stands as a mathematical legacy perpetually impacting our daily lives, influencing architecture, engineering, and shaping our perception of space and object relationships.
On the TeMa platform, online math tutors await, ready to guide you in unraveling the secrets of this captivating scientific field. Mathematical knowledge serves as a gateway to myriad possibilities, and with TeMa, learning becomes even more accessible. Brace yourself for an enthralling expedition through the realm of mathematics, where geometric enigmas serve as keys to comprehending the world around you. Best of luck!