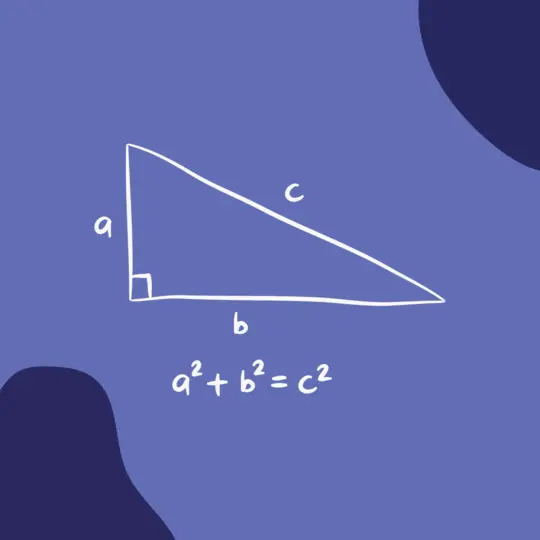Мы рады, что вы посвятили время погружению в увлекательную область геометрической математики и разгадке тайн теоремы Пифагора. Без дальнейшего промедления давайте углубимся в изучение и понимание этого необычного утверждения. Квадрат суммы катетов равен квадрату длины гипотенузы. Дополнительно ее можно сравнить с польской пословицей: «Мудрость заключается в простоте, как квадрат в математике». Теорема Пифагора является краеугольным камнем геометрической математики и демонстрирует множество удивительно универсальных приложений. В рамках этого исследования мы исследуем суть этой теоремы, рассмотрим его фундаментальные принципы, особенности, применение как в математическом контексте, так и в повседневных сценариях, а также его значение в сфере строительства и архитектуры.
Причины выучить теорему Пифагора:
- Это выходит за рамки простого математического дискурса; он служит ключевыми воротами к более сложным предметам.
- Откройте для себя его разнообразную полезность в таких областях, как физика, навигация, информатика и даже искусственный интеллект — инструмент, выходящий за рамки математики.
- От измерения расстояний на картах до формирования внутреннего пространства — он оказывает влияние на наш повседневный выбор и действия. Откройте для себя ощутимые преимущества, которые можно извлечь из этой математической жемчужины.
- Без теоремы Пифагора многие монументальные сооружения просто не существовали бы.
Раскрытие основной концепции теоремы Пифагора: фундаментальные идеи в одном снимке
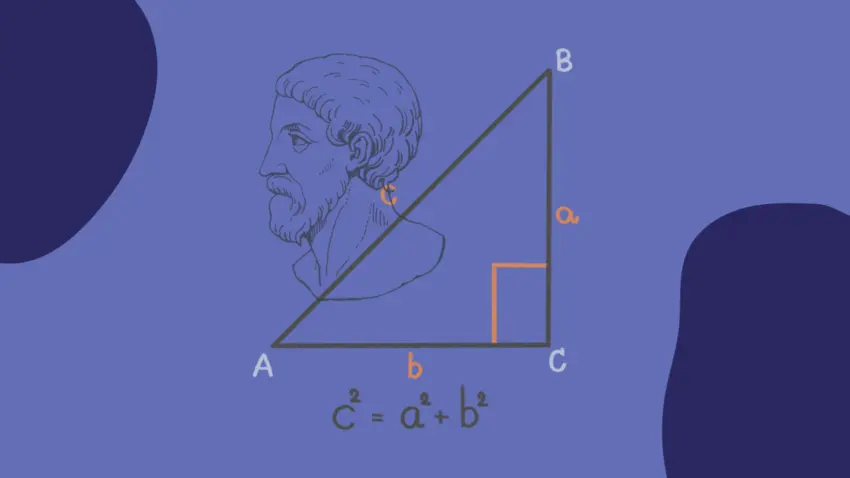
В основе математики, особенно в контексте прямоугольных треугольников, лежит теорема Пифагора — основополагающий принцип. Вкратце, он утверждает, что в таких треугольниках квадрат длины гипотенузы равен сумме квадратов длин катетов. Математически это выражается уравнением Пифагора.
с2 =а2 + b2
Это, казалось бы, простое, но очень мощное выражение служит воротами к пониманию взаимосвязей между сторонами треугольников, облегчая широкий спектр приложений в различных математических областях и повседневных сценариях. Он действует как метафорический ключ, открывающий богатства, скрытые в математической сфере, и направляющий нас к более глубокому пониманию тонкостей геометрического пространства.
Интригующие факты о теореме Пифагора
Приступая к увлекательному исследованию загадочных сфер теоремы Пифагора, следует отметить, что ее истоки выходят за пределы Древней Греции. Это математическое чудо нашло признание и применение в различных культурах, включая египетское, китайское и вавилонское общества.
В Древнем Египте математики занимались аналогичными геометрическими отношениями, подчеркивая, что концепции, связанные с теоремой Пифагора, выходят за рамки конкретных регионов и эпох. Китайцы также внесли заметный вклад в это дело, подтвердив универсальную природу математики и ее функцию как межконтинентального языка общения.
То, что мы сейчас называем теоремой Пифагора, имело значение в вавилонской математике, особенно в исследовании прямоугольных треугольников для практических приложений в таких областях, как астрономия и строительство.
Все эти примеры подчеркивают, что привлекательность теоремы Пифагора всеобъемлюща, превосходя временные и пространственные ограничения. Она возникает не просто как фрагмент математической истории, но и как захватывающая одиссея через богатое разнообразие культур и их ключевую роль в развитии научных знаний.
Применение теоремы Пифагора в математике и повседневных ситуациях
Основная область применения этой теоремы — решение проблем, связанных с прямоугольными треугольниками. Его полезность заключается в облегчении прямого вычисления длин сторон треугольника, когда известны две другие длины. Этот ресурс служит фундаментальной отправной точкой для изучения взаимодействия между углами и сторонами внутри этого конкретного типа треугольника.
Однако значение теоремы Пифагора выходит за рамки плоской геометрии. В области математики он также используется для вычисления расстояний между точками в трехмерном пространстве. Это особенно полезно в декартовой системе координат, где расстояния между точками определяются с помощью прямоугольных треугольников.
Решение геометрических задач с помощью теоремы Пифагора
В сценариях решения задач учащимся поручено тщательно изучить данную ситуацию, определить известные и неизвестные значения и впоследствии использовать теорему для получения решения.
Акцент выходит за рамки простого запоминания уравнений и вычислений Пифагора; оно включает в себя развитие навыков логического мышления. Учащиеся приобретают способность систематически и точно решать геометрические задачи, навыки, выходящие за рамки математики и позволяющие решать задачи в повседневной жизни.
Теорема предполагает двойную роль: она служит не только математическим инструментом, но и катализатором развития когнитивных навыков, применимых в различных сферах жизни. Он тонко преподает уроки по применению логического подхода к решению проблем, формируя остроту ума учащихся для будущих начинаний.
Историческое путешествие и эволюция теоремы Пифагора
Понимание, полученное в ходе исторического путешествия и эволюции теоремы Пифагора, вселяет глубокое восхищение этим математическим шедевром. Охватывая период от Древней Греции до наших дней, эта теорема не только сохраняется, но и развивается, отвечая новым вызовам и контекстуальным требованиям.
Сегодняшнее размышление над теоремой Пифагора приводит к осознанию того, что она выходит за рамки единственного математического утверждения; это фрагмент истории, не поддающийся временным и пространственным ограничениям. Оно представляет собой математическое наследие, постоянно влияющее на нашу повседневную жизнь, влияющее на архитектуру, инженерию и формирующее наше восприятие пространства и отношений между объектами.
На платформе TeMa вас ждут онлайн преподаватели по математике, готовые помочь вам разгадать секреты этой увлекательной научной области. Математические знания служат воротами к множеству возможностей, а с TeMa обучение становится еще более доступным. Приготовьтесь к увлекательному путешествию по миру математики, где геометрические загадки служат ключом к пониманию окружающего мира. Удачи!