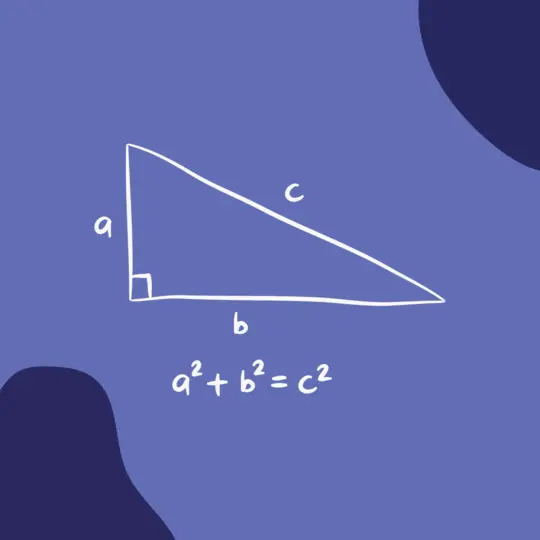Cieszymy się, że znaleźliście czas, aby zanurzyć się w fascynujący świat matematyki geometrycznej i odkryć tajemnice Twierdzenia Pitagorasa. Kwadrat sumy przyprostokątnych odpowiada kwadratowi długości przeciwprostokątnej. Dodatkowo może być to porównane do polskiego przysłowia: „Mądrość w prostocie tkwi jak kwadrat w matematyce". Bez dalszego przedłużania, zanurzmy się głębiej w analizę i zrozumienie tego niezwykłego twierdzenia. Twierdzenie Pitagorasa stanowi fundament matematyki geometrycznej, a jego zastosowania są niezwykle wszechstronne. W niniejszej analizie zgłębimy istotę tego twierdzenia, przyjrzymy się jego podstawom, ciekawostkom, zastosowaniom matematyce i życiu codziennym, a także roli, jaką odgrywa budownictwie, architekturze.
Dlaczego warto zgłębiać Twierdzenia Pitagorasa:
- To nie tylko zdanie matematyczne, ale klucz do otwarcia drzwi do bardziej zaawansowanych zagadnień.
- Odkryj, jak może być używane różnych dziedzinach, takich jak fizyka, nawigacja, informatyka czy nawet sztuczna inteligencja. To narzędzie, które przekracza granice matematyki.
- Od pomiaru odległości na mapie po projektowanie wnętrz, wpływa na nasze codzienne decyzje i czynności. Poznaj, jakie praktyczne korzyści możemy czerpać z tej matematycznej perły.
- Bez Twierdzenia Pitagorasa nie byłoby wielu monumentalnych konstrukcji.
Istota Twierdzenia Pitagorasa: Podstawy w Skrócie
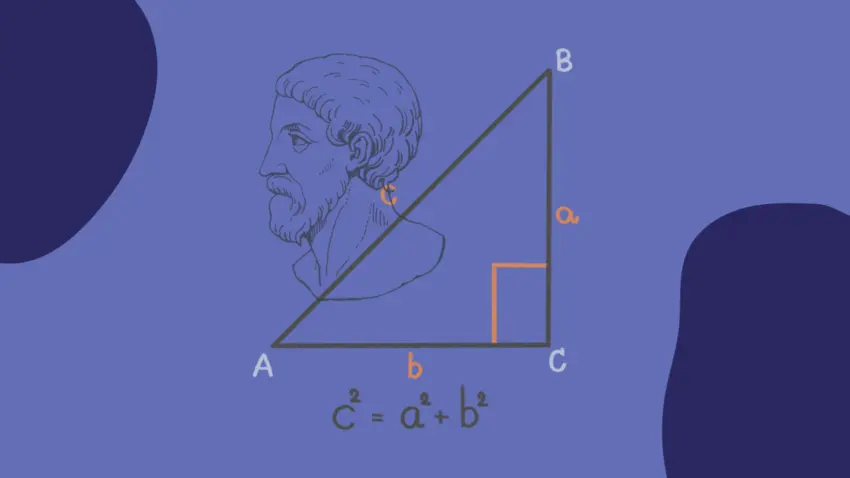
Twierdzenie Pitagorasa stanowi kluczowy filar matematyki, szczególnie gdy mówimy o trójkątach prostokątnych. W zwięzły sposób głosi, że w takim trójkącie kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych. Wyrażając to matematycznie, używamy równania Pitagorasa.
c2 =a2 +b2
To proste, ale niezwykle potężne zdanie, które otwiera drzwi do zrozumienia relacji między bokami trójkątów i umożliwia szerokie spektrum zastosowań w różnych dziedzinach matematyki oraz życiu codziennym. To jak klucz, który odblokowuje skarby matematycznego świata, prowadząc nas ku głębszemu zrozumieniu struktury przestrzeni geometrycznej.
Ciekawostki Dotyczące Twierdzenia Pitagorasa
Podczas fascynującej podróży w głąb tajemnic Twierdzenia Pitagorasa, warto zauważyć, że jego korzenie sięgają nie tylko starożytnej Grecji. To matematyczne arcydzieło było również znane i stosowane w innych kulturach, w tym egipskiej, chińskiej i babilońskiej.
W starożytnym Egipcie matematycy posługiwali się podobnymi zależnościami geometrycznymi, co potwierdza, że idee związane z Twierdzeniem Pitagorasa przekraczały granice jednego regionu czy epoki. Chińczycy również mieli swoje własne odkrycia związane z tym zagadnieniem, co dowodzi uniwersalności matematyki i jej roli jako języka porozumiewania się na różnych kontynentach.
To, co dzisiaj nazywamy Twierdzeniem Pitagorasa, stanowiło istotny element matematyki babilońskiej. Ich prace nad trójkątami prostokątnymi ukierunkowane były na praktyczne zastosowania w dziedzinach związanych z astronomią i budownictwem.
Wszystko to pokazuje, że magia Twierdzenia Pitagorasa jest uniwersalna i przekracza granice czasu oraz przestrzeni. To nie tylko fragment historii matematyki, ale także fascynująca podróż przez różnorodność kultur i ich wkład w rozwój nauki.
Zastosowanie Twierdzenia Pitagorasa w Matematyce i Życiu Codziennym
Podstawowym obszarem wykorzystania tego twierdzenia jest rozwiązywanie problemów związanych z trójkątami prostokątnymi. Dzięki niemu możemy łatwo obliczać długości boków trójkąta, znając długości dwóch z nich. To narzędzie staje się kluczowym punktem wyjścia przy analizie relacji między kątami a bokami tego specyficznego rodzaju trójkąta.
Jednak rola Twierdzenia Pitagorasa nie kończy się na geometrii płaskiej. W matematyce stosuje się je również do obliczania odległości między punktami w przestrzeni trójwymiarowej. To przydatne narzędzie w kartezjańskim układzie współrzędnych, gdzie wyznacza się dystanse między punktami, korzystając z trójkątów prostokątnych.
Zadania Geometryczne z Użyciem Twierdzenia Pitagorasa
W trakcie rozwiązywania problemów uczniowie muszą precyzyjnie analizować daną sytuację, identyfikować znane i nieznane wartości, a następnie wykorzystywać twierdzenie w celu znalezienia rozwiązania.
To nie tylko nauka równań i obliczanie Pitagorasa, ale także rozwijanie umiejętności logicznego myślenia. Uczniowie uczą się, jak podejść do zagadnienia geometrycznego w sposób systematyczny i precyzyjny, co ma zastosowanie nie tylko w matematyce, ale także w rozwiązywaniu problemów w życiu codziennym.
Twierdzenie staje się nie tylko narzędziem matematycznym, ale także katalizatorem rozwijania umiejętności myślowych, które są cenne w różnych dziedzinach życia. To także subtelna lekcja logicznego podejścia do rozwiązywania problemów, co kształtuje umysł uczniów na przyszłość.
Historia i Ewolucja Twierdzenia Pitagorasa
Lekcje matematyki wyciągnięte z historii i ewolucji twierdzenia Pitagorasa dają nam głęboki szacunek dla tego matematycznego arcydzieła. Od starożytnej Grecji po dzień dzisiejszy twierdzenie to nie tylko przetrwało, ale także ewoluowało, dostosowując się do nowych wyzwań i kontekstów.
Kiedy dziś myślimy o Twierdzeniu Pitagorasa, warto rozpoznać, że nie jest to tylko jedno zdanie matematyczne, ale kawałek historii wykraczający poza czas i przestrzeń. Jest to dziedzictwo matematyczne, które wciąż wpływa na nasze codzienne życie, architekturę, inżynierię oraz sposób, w jaki myślimy o przestrzeni i relacjach między obiektami. Na platformie TeMa znajdziesz korepetycje online matematyka, którzy pomogą Ci odkryć tajemnice tej fascynującej dziedziny nauki. Wiedza matematyczna otwiera drzwi do wielu możliwości, a dzięki TeMa nauka staje się jeszcze bardziej dostępna. Przygotuj się na ekscytującą podróż po krainie matematyki, gdzie geometryczne zagadki stają się kluczem do zrozumienia otaczającego Cię świata. Powodzenia!